avertissement¶
pour le confort de chacun, veuillez vous assurer avant de commencer que le volume de votre haut parleur est réglé au minimum audible pour vous :)
imports¶
import numpy as npimport matplotlib.pyplot as plt
# en mode interactif ça peut être utile de choisir un mode interactif
# comme par exemple celui-ci
# par contre ça nécessite de faire un `pip install ipympl`
# %matplotlib ipympl# pour jouer le son qu'on va produire
from IPython.display import Audionature du son¶
comme vous le savez sans doute, lorsqu’on enregistre un morceau de musique, on capture la position de la membrane du microphone au cours du temps
puisqu’il s’agit de son, la membrane oscille autour de sa position d’équilibre, dans un mouvement pseudo-périodique, et la fréquence à un moment donné détermine la hauteur du son qu’on entend
ainsi la fréquence de 440Hz a été définie comme étant la fréquence du LA (enfin pour être précis, d’un LA, on y reviendra)
comment on capture du son¶
une technique pour enregistrer le son consiste à simplement capturer la position de la membrane à intervalles réguliers : on appelle cela l’échantillonnage, qui produit en sortie une collection de valeurs numériques
les fréquences audibles sont comprises, disons, pour être très large, entre 20 Hz et 20 kHz
du coup pour ne pas perdre en précision, on échantillonne traditionnellement à une fréquence de 44.1 kHz (chiffre qui date de l’époque des CD)
ce qui signifie que si on produit un tableau de 44100 valeurs qui représentent une sinusoïde parfaite, on pourra jouer cela comme un son de 1s et sur une note continue; ce sera notre premier exercice
RATE = 44_100
LA = 440synthétiseur - fréquence¶
reste à déterminer l’amplitude, pour l’instant on prend une amplitude de 1
imaginons que nous voulions produire un son correspondant à un LA à 440 Hz, sur une seconde:
- nous devons donc calculer un tableau qui fait combien d’entrées ?
- quelle est en fonction du temps, et donc sur l’intervalle ,
l’équation de la fonction qui nous intéresse ? - comment on peut s’y prendre pour calculer ce tableau ?
Tip
la fonction qui donne la position de la membrane en fonction du temps est, si ϕ représente la fréquence du son
# bien sûr ce n'est pas comme ça qu'il faut faire
# mais pour que la suite soit vaguement cohérente
# et que l'énoncé ne contienne pas des milliers d'erreurs...
la_1seconde = np.arange(RATE) / RATE# votre code
# la_1seconde = ...# pour écouter le résultat
# remarquez qu'on a maintenant perdu la fréquence d'échantillonnage
# il faut repasser cette information au lecteur de musique
Audio(la_1seconde, rate=RATE)commodité
comme on ne va produire que des sons échantillonnés à 44.100 Hz, ce sera plus commode de ne pas avoir à le répéter à chaque fois
def MyAudio(what, **kwds):
return Audio(what, rate=RATE, **kwds)MyAudio(la_1seconde)MyAudio(la_1seconde, autoplay=True)on en fait une fonction¶
pour généraliser un petit peu, on va écrire une fonction
qui produit un son sinusoïdal, et qui prend en paramètres
la fréquence et la durée
Tip
commencez par vous demander combien d’échantillons on doit produire
# pareil ici: je donne une implémentation folklorique
# pour ne pas avoir plein d'erreurs dans l'énoncé
def sine(freq, duration=1, amplitude=1.):
return la_1seconde# votre code
# def sine(freq, duration=1, amplitude=1.):
# ...# pour écouter: plus court
MyAudio(sine(LA, .5), autoplay=True)# pour écouter: plus long
MyAudio(sine(LA, 1.5), autoplay=True)pour les rapides¶
on veut obtenir un effet de ‘note qui monte’
améliorer un peu pour générer une courbe avec un fréquence qui croit (ou décroit) linéairement avec le temps
écrire une fonction sine_linear(freq1, freq2, duration)
# votre code
def sine_linear(freq1, freq2, duration):
...# pour écouter
MyAudio(sine_linear(440, 660, 3))---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
Cell In[16], line 2
1 # pour écouter
----> 2 MyAudio(sine_linear(440, 660, 3))
Cell In[8], line 2, in MyAudio(what, **kwds)
1 def MyAudio(what, **kwds):
----> 2 return Audio(what, rate=RATE, **kwds)
File ~/.local/lib/python3.12/site-packages/IPython/lib/display.py:115, in Audio.__init__(self, data, filename, url, embed, rate, autoplay, normalize, element_id)
112 def __init__(self, data=None, filename=None, url=None, embed=None, rate=None, autoplay=False, normalize=True, *,
113 element_id=None):
114 if filename is None and url is None and data is None:
--> 115 raise ValueError("No audio data found. Expecting filename, url, or data.")
116 if embed is False and url is None:
117 raise ValueError("No url found. Expecting url when embed=False")
ValueError: No audio data found. Expecting filename, url, or data.réglage du volume¶
crescendo¶
imaginons qu’on veuille produire un son de plus en plus fort
par exemple qui monte crescendo de manière linéaire
sur toute la durée du son
- comment on pourrait faire ça ?
# votre code pour 1.
crescendo_la_1seconde = ...# pour écouter
MyAudio(crescendo_la_1seconde) #, autoplay=True)en faire une fonction
def crescendo_sine(freq, duration): ...
# votre code pour 2.
def crescendo_sine(freq, duration):
...# pour écouter
MyAudio(crescendo_sine(LA, 2)) #, autoplay=True)- ajouter un paramètre pour pouvoir décroître
def crescendo_sine(freq, duration, increase=True): ...
# votre code pour 3.
def crescendo_sine(freq, duration, increase=True):
...# pour écouter
MyAudio(crescendo_sine(LA, 2, increase=False)) #, autoplay=True)- avancés: est-ce qu’on ne pourrait pas faire un choix un peu plus malin ?
# votre code pour 4.
...concaténation¶
on sait maintenant produire des notes élémentaires
sachant que la note DO immédiatement au dessus du la-440 a une fréquence de l’ordre de 523 Hz, comment pourrait-on maintenant produire une succession de deux notes la et do ?
# la fréquence du DO
DO = 523.25# votre code
la_do = ...# pour écouter
MyAudio(la_do, autoplay=True)amplitude et types¶
jusqu’ici, chaque échantillon est représenté par un nombre flottant entre -1 et 1
il se trouve que ça n’est pas forcément le plus pertinent comme approche, notamment lorsqu’il va s’agir de sauver notre son sur fichier
aussi nous allons maintenant nous poser la question de changer d’échelle - et de type de données - pour utiliser plutôt des entiers 16 bits (que pour rappel on a à notre disposition avec numpy.int16)
entiers signés ou non¶
ce qui nous amène à une petite digression: profitons-en pour regarder un peu comment sont encodés les entiers;
l’encodage des entiers signés fonctionne comme suit; on regarde ici les types int8 et uint8 car c’est plus simple, le principe est exactement le même pour des tailles plus grandes
il y a deux types d’encodages pour les entiers, signés (int8) et non signés (uint8, le u signifie unsigned)
les entiers non signés sont simples à encoder, avec 8 bits on peut aller de 0 à 255
par contre pour les entiers signés, on va devoir utiliser un bit comme bit de signe, ce qui limite le spectre de ce qu’il est possible d’encoder; avec en tout 8 bits on peut encoder de -128 à 127 inclus.
| entier | int8 | uint8 |
|---|---|---|
| -128 | 10000000 | n/a |
| -127 | 10000001 | n/a |
| -126 | 10000010 | n/a |
| ... | ||
| -003 | 11111101 | n/a |
| -002 | 11111110 | n/a |
| -001 | 11111111 | n/a |
| ------- | ||
| 000 | 00000000 | 00000000 (idem) |
| 001 | 00000001 | 00000001 (idem) |
| 002 | 00000010 | 00000010 (idem) |
| ... | ||
| 125 | 01111101 | 01111101 (idem) |
| 126 | 01111110 | 01111110 (idem) |
| 127 | 01111111 | 01111111 (idem) |
| ------- | ||
| 128 | n/a | 10000000 |
| 129 | n/a | 10000001 |
| 130 | n/a | 10000011 |
| ... | ||
| 253 | n/a | 11111101 |
| 254 | n/a | 11111110 |
| 255 | n/a | 11111111 |
du coup avec le type int16 on va pouvoir encoder l’intervalle [-32768, 32767]
2**15ça veut dire que si on sort de cet intervalle on va avoir des surprises
# à vousmise à l’échelle¶
exercice
en vous souvenant qu’on a à notre disposition la méthode array.astype()
pour fabriquer une copie d’un tableau numpy convertie dans un autre type,
écrivez une fonction qui transforme
notre tableau de flottants dans [-1, 1].
en un tableau d’entiers signés 16bits
et pour préserver le niveau sonore, il faut que les entrés maximales
i.e. 1 ou -1 dans le 1er format
correspondent au maximum codable dans le second format
le son produit doit être totalement identique - le volume notamment
# votre code
def float_to_int16(as_float):
...# pour écouter
MyAudio(float_to_int16(la_do), autoplay=True)# sans conversion
MyAudio(la_do, autoplay=True)fréquences des notes de la gamme¶
dans cette partie, nous allons calculer les fréquences des notes
pour les non-musiciens, sachez que, pour simplifier :
gamme chromatique¶
la gamme chromatique (toutes les notes du piano) contient 12 notes
・ ・ ・ ・ ・ ・ ・ ・ ・ ・ ・
séparées de 1/2 ton
(le s’appelle aussi mais c’est une autre histoire...)
et si on rajoute la note suivante (qu’on appelle ), cela fait 13 notes donc 12 intervalles
intervalles¶
notre oreille reconnait bien les intervalles entre deux notes
par exemple si vous jouez les deux extraits ci-dessous
vous allez reconnaitre dans les deux cas le pin-pon des pompiers
Audio(filename='media/pin-pon-la-si.wav')Audio(filename='media/pin-pon-fa-sol.wav')ici dans les deux cas, les deux notes utilisées (la - si, puis fa - sol)
sont dans les deux cas séparées de 2 crans dans la gamme chromatique
(on dit que les deux notes constituent un intervalle de 2 demi-tons, soit un ton)
et comme c’est le même intervalle, notre oreille entend dans les deux cas la même “mélodie”
un intervalle = un rapport entre fréquences¶
enfin, il faut savoir que ce qui caractérise un intervalle, c’est le rapport entre les fréquences des deux notes
ainsi par exemple, vous pouvez constater que si on multiplie une fréquence par 2
# une octave de LA
MyAudio(
np.concatenate((sine(LA, 0.5),
sine(2*LA, 0.5))),
autoplay=True)on entend une note qui ressemble beaucoup à la premiére
en réalité, le fait de multiplier la fréquence par 2
permet d’obtenir une note une octave au dessus
(c’est-à-dire de passer d’un DO au DO au dessus)
# même effet avec le DO naturellement
MyAudio(
np.concatenate((sine(DO, 0.5),
sine(2*DO, 0.5))),
autoplay=True)calculons les fréquences des notes¶
on a toutes les informations à ce stade pour calculer
les fréquences des notes de la gamme (dite bien tempérée)
en effet on sait que, puisque c’est toujours le même intervalle,
un demi-ton correspond à un rapport constant entre les (fréquences des) notes
qu’on va appeler α
et comme par ailleurs on sait qu’entre les deux do il y a une octave donc
mais c’est aussi
d’où il ressort que
exercices
- calculer - sans boucle for - un tableau contenant
les 13 - de do à do’ inclus -
rapports entre do et les notes de la gamme
(ratios[0]devrait valoir 1, etratios[12]devrait valoir 2)
- on a besoin d’une fonction qui calcule la fréquence
d’une note à partir de son nom
on veut bien sûr que
scale = ['do', 'do#', 'ré', 'ré#', 'mi', 'fa', 'fa#', 'sol', 'sol#', 'la', 'la#', 'si']# votre code
def freq_from_name(name):
...# pour vérifier: devrait retourner
# ou presque (rappelez-vous les erreurs d'arrondi avec les flottants)
freq_from_name('la')# attention à la précision !
freq_from_name('la') == 440# question: on fait comment déjà pour comparer deux flottants ?
# à vousTip
pensez à utiliser ceci np.isclose(freq_from_name('la'), 440)
rationnels approchants¶
pour comprendre les harmonies, ce qui intéressant
c’est que parmi les ratios qu’on a calculés plus haut,
certains sont très proches de rapports rationnels simples
il n’y a pas d’exercice dans cette section, juste un exemple de visualisation
# intervalle do-mi (tierce majeure) ~= 5/4
ratios[4]# intervalle do-sol (quinte) ~= 3/2
ratios[7]visuel (1)¶
pour visualiser les ratios de la gamme
(uniquement des exemples d’utilisation de matplotlib)
plt.figure(figsize=(2, 6))
# on veut afficher 12 points de coordonnées
# tous avec une coordonnée X=0
X = np.zeros(ratios.shape)
# et pour marqueur un petit trait horizontal
plt.scatter(X, ratios, marker=0, linewidth=0.5);visuel (2)¶
pareil, mais en superposant les rationnels , et
# on remarque quelques rapports proches
specials = np.array([1, 5/4, 4/3, 3/2, 2])# pour dessiner des traits un peu plus beaux
# où on contrôle la taille et l'épaisseur
def strike(height, width, color, linewidth):
plt.plot([-width, width], [height, height],
color=color, linewidth=linewidth)
def turn_off_xticks():
plt.tick_params(
axis='x', # changes apply to the x-axis
which='both', # both major and minor ticks are affected
bottom=False, # ticks along the bottom edge are off
top=False, # ticks along the top edge are off
labelbottom=False) # labels along the bottom edge are off# on crée une figure
plt.figure(figsize=(2, 6))
# on enlève les marques sur l'axe des X
turn_off_xticks()
# on dessine les notes de la gamme en orange
for ratio in ratios:
strike(ratio, 0.1, 'orange', 0.5)
# et les quelques rapports qu'on a remarqués à l'oeil nu
for special in specials:
strike(special, 0.2, 'blue', 0.2)superposer deux sons¶
comment faire pour jouer plusieurs sons en même temps ?
do = sine(freq_from_name('do'), 2)
mi = sine(freq_from_name('mi'), 2)
sol = sine(freq_from_name('sol'), 2)# votre code
accord_do_mi_sol = ...# pour écouter
MyAudio(accord_do_mi_sol, autoplay=True)sauver un son dans un .wav¶
on peut facilement sauver nos sons
grâce à la librairie scipy
par contre il faut savoir que le format le plus robuste
est celui qui utilise les entiers 16 bits qu’on a vus plus haut
from scipy.io import wavfileexercice
- chercher dans la documentation comment sauver un son dans un fichier
.wav - sauver un de vos morceaux (par exemple
la_do) - relisez-le
- assurez-vous que le résultat est conforme au morceau de départ
# votre code
original = la_do # par exemple
#
# sauver le son 'before' dans un fichier 'sample.wav'
#
restored = ... # relisez le fichier 'sample.wav' dans une variable 'after'# pour vérifier
MyAudio(original)# pour vérifier
MyAudio(restored)un vrai son¶
on part d’un petit fichier media/sounds-cello.wav
exercice
- lire le fichier (ranger le signal dans une variable
data) (voyezwavfile.read)
# votre code- écoutez le
# votre code- afficher le samplerate utilisé dans le fichier
# votre code- afficher le nombre d’échantillons
# votre code- afficher la longueur du morceau en secondes
# votre codeà quoi ça ressemble¶
on va utiliser matplotlib pour afficher le signal
affichez le signal du morceau (la position de la membrane) en fonction du temps à l’aide de la fonction plt.plot()
- c’est important d’avoir un rendu interactif (souvenez vous de
%matplotlib) - pour pouvoir zoomer dans le diagramme
- notamment utiles: pour zoomer (icône carrée), déplacer (les deux flêches croisées), revenir au point de vue de départ (la maison)..
effet d’echo¶
maintenant on veut ajouter un effet d’echo
il nous faut pour cela
- créer une version du son initial, mais décalée dans le temps
- et ajouter les deux
sauf que si on s’y prend comme cela:
les deux signaux apparaissent avec le même niveau sonore
or un effet d’echo sous-entend une atténuation du signal tardifen plus avec le type
int16, on risque de causer des erreurs de débordement
en effet si au même instant les deux signaux contiennent tous deux
une valeur >= 20_000, la somme va dépasser 215 et donc provoquer
une conversion et donc une erreur
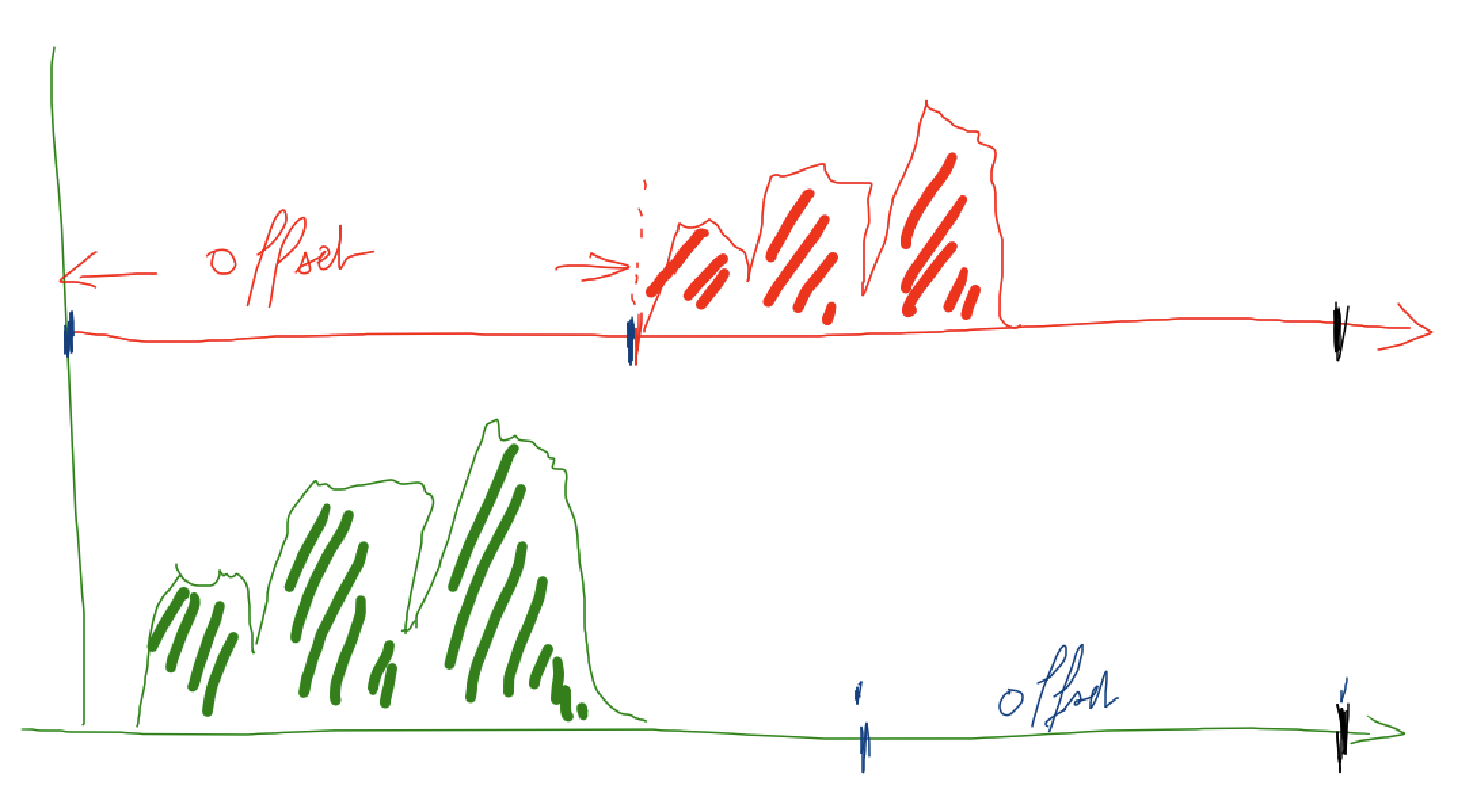
c’est ce qu’on essaie d’illustrer ici
le signal de départ (en vert)
est décalé vers la droite de la valeur du retard
et on applique à chacun une pondération
par exemple 70% pour le signal de départ, et 30% pour le signal retardéavant de les ajouter
# quelques constantes
# en seconde
delay = 2
# les deux ratios
main_ratio, delayed_ratio = 0.7, 0.3exercice v1
- traduire
delayen nombre d’échantillonsoffset - produire le son avec echo, sur une durée correspondant au son de départ
# votre code pour produire
# le son de 'data' avec echo
data_echoed = ...# pour écouter
MyAudio(data_echoed)# pour observer
plt.figure(figsize=(12, 4))
plt.plot(data_echoed, linewidth=0.05);exercice v2
- idem mais pour produire une durée un peu plus longue, correspondant à la somme
- de la durée du son de départ
- et du retard
# votre code
data_echoed_v2 = ...# pour écouter
MyAudio(data_echoed_v2)# pour observer
plt.figure(figsize=(10, 4))
plt.plot(data_echoed_v2, linewidth=0.05);transposer¶
transposer d’une octave¶
on a vu qu’une octave correspond à une fréquence deux fois plus élevée
partant de par exemple data, comment produire un son une octave au dessus ?
(on s’astreint à ne pas modifier le samplerate)
je vous laisse y réfléchir un moment...
pour élever d’une octave, il suffit d’ignorer un échantillon sur deux
pourquoi ? de cette façon on va artificiellement
- diminuer la durée par 2 (2 fois moins d’échantillons, toujours à la même fréquence d’échantillonage de 44.100 Hz)
- et du coup multiplier par 2 la fréquence des sons perçus
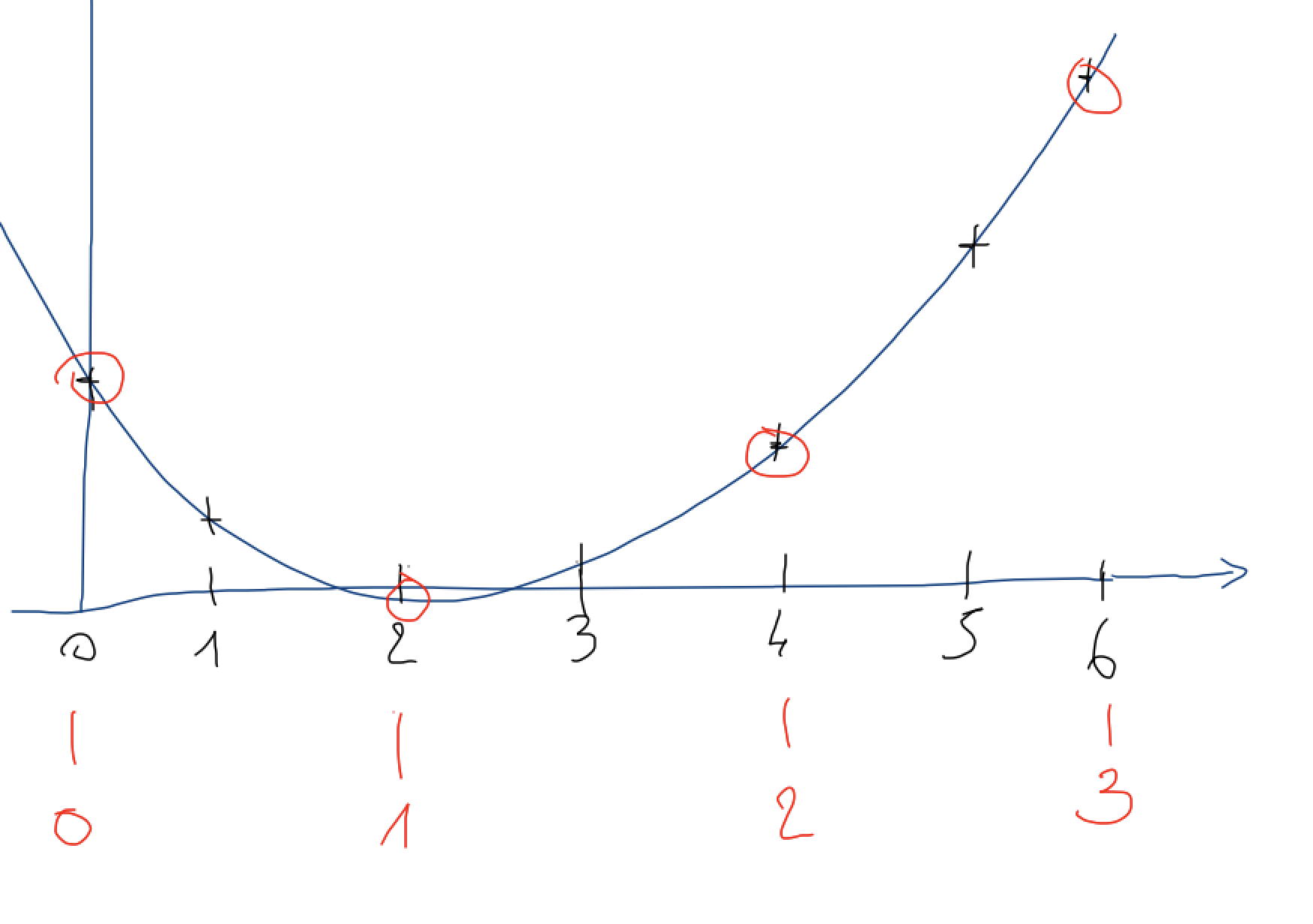
exercice
fabriquer un son qui soit similaire à celui dans data, mais une octave au dessus
# votre code ici
data2 = ...# pour écouter
MyAudio(data)# pour écouter
MyAudio(data2)naturellement le profil reste le même mais l’échelle des X est plus courte (deux fois moins d’échantillons)
plt.figure(figsize=(10, 4))
plt.plot(data2, linewidth=0.05);transposer d’une quinte¶
pour transposer d’une quinte, il nous faut multiplier la fréquence par 3/2; on peut utiliser une approche voisine
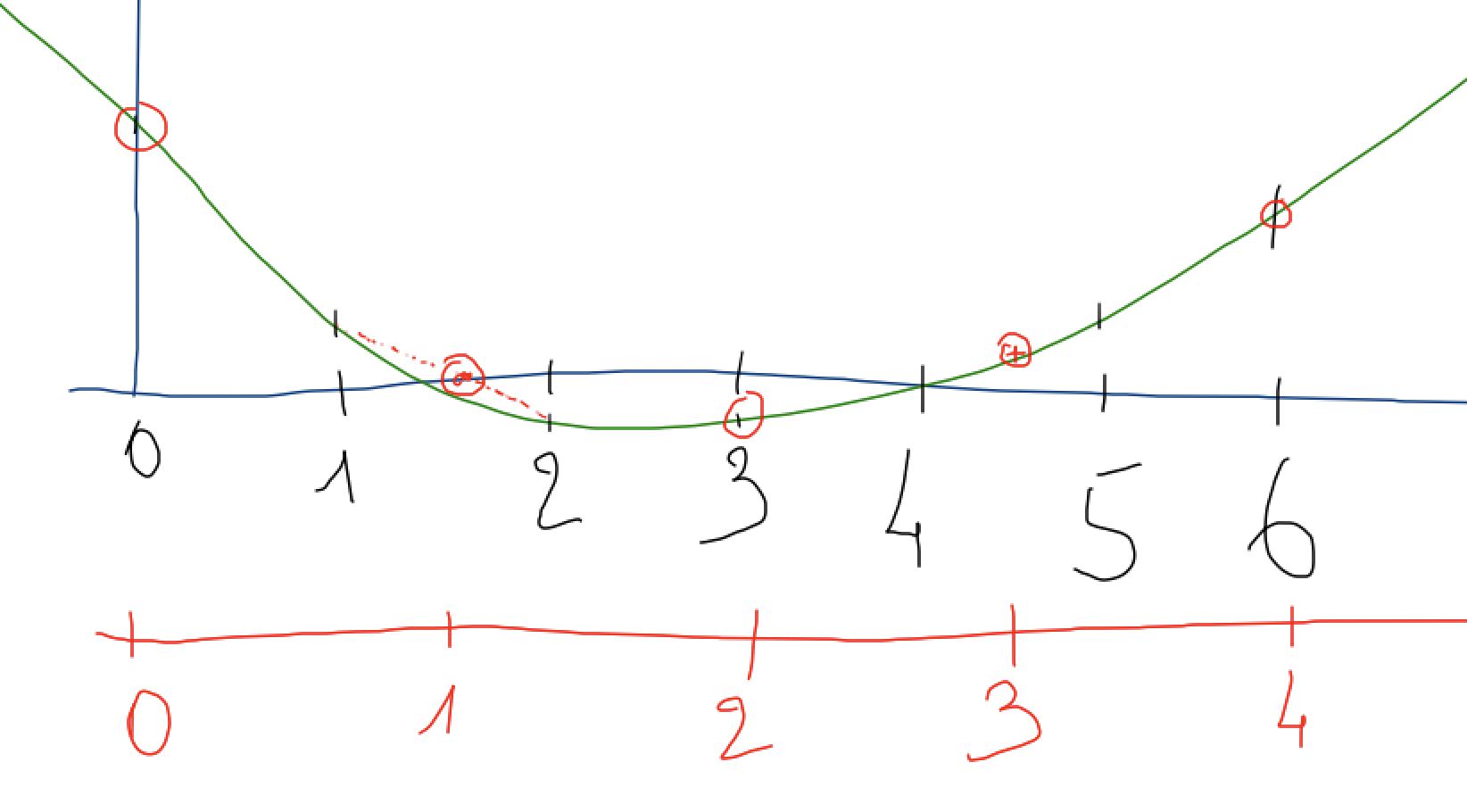
sauf que cette fois, il faut un peu interpoler; on est donc amené à faire des moyennes comme ceci
data data3
0 0 0
1 1+2/2 1
2 --
3 3 2
4 4+5/2 3
5 --
...exercice appliquez l’idée ci-dessus :
- créez un tableau
data3dont la taille est 2/3 de celle dedata - remplir dans
data3les données de rang pair
qui correspondent aux multiples de 3 dans le tableau de départ - remplir dans
data3les données de rang impair
en implémentant l’interpolation
remarque: nos data sont en int16, on va s’efforcer
de continuer à travailler dans ce format
# votre code
data3 = ...# vérification de visu
# ces deux segments correspondent normalement
# au même instant dans le morceau
data[12000:12007], data3[8000:8005]# pour écouter
MyAudio(data3)la fraction la plus proche (avancés - sans exercice)¶
on peut s’amuser à calculer, pour chaque note, la fraction la plus proche - si on se restreint à des rationnels avec un dénominateur “petit”
pour ça on se fixe par exemple N=7 et pour chaque note x, on veut minimiser abs(x-r) pour r étant dans l’espace
si on voulait faire ça en Python pur, on pourrait écrire quelque chose comme
from fractions import FractionN = 7
# tous les rationnels concernés dans [1, 2[
rationals = {1 + Fraction(p, q) for q in range(1, N+1) for p in range(q+1)}
rationals# la version la plus rapide à écrire
def closest1(note):
return min(abs((note-rational)/rational) for rational in rationals)# mais le souci c'est qu'on a perdu de l'information
tierce, quinte = ratios[4], ratios[7]
closest1(quinte)# du coup ça se complique un peu
def closest2(note):
minimum = np.inf
result = None
for rational in rationals:
if abs(note-rational) < minimum:
minimum = abs(note-rational)/note
result = rational
return result, minimumclosest2(quinte)# encore une autre version
def closest(note):
"""
on retourne le rationnel le plus proche
avec l'erreur relative que ça représente
sous la forme d'un tuple
(rationnel, erreur relative)
"""
# on va trier une liste de tuples (rational, relative_error)
# c'est sous-optimal d'un point de vue algorithmique
# car on n'a pas vraiment besoin de trier toute la liste
# dans ces ordres de grandeur ça n'a pas bcp d'importance
# par contre ça donne un code un peu plus intéressant
candidates = [(rational, abs(note-rational)/note) for rational in rationals]
return sorted(candidates, key=lambda couple: couple[1])[0]closest(quinte)les accords harmonieux¶
si on ne garde que les notes qui sont très proches - avec une erreur relative de moins de 0.5%
on trouve les intervalles do-fa et do-sol