indexation avancée

import numpy as np

contenu de ce notebook (notebook optionnel)¶

on a vu jusqu’ici comment indexer un tableau (quand on écrit valeurs[indices]):

• quand indices est un masque
• et quand indices est un entier, une slice (ou un tuple qui contient des entiers ou tuples)

ce que nous appelons ici indexation avancée,
c’est la possibilité d’indexer un tableau avec .. un ou plusieurs autres tableaux d’entiers
c’est-à-dire d’écrire array1[array2] ou encore array1[(array2, array3)]

valeurs en dimension 1¶

valeurs_d1 = 10 * np.arange(5)
valeurs_d1

voyons le cas le plus simple, de forme array1[array2]

on va pouvoir indexer valeurs par n’importe quel tableau qui ne contient que des entiers entre 0 et 4
(parce qu’ils seront interprétés comme des indices dans valeurs qui est de taille 5)

et le résultat de valeurs[indices] va être un tableau de la même forme qu’indices
et qui contiendra les valeurs[indice] pour chaque case indice de indices

c’est donc en quelque sorte la version vectorisée de l’indexation par un entier...

# par exemple si indices est un vecteur, on récupère un vecteur
indices = np.array([0, 2, 3, 1, 3, 1, 2, 0, 3, 2, 3])

valeurs_d1[indices]

# par exemple, si le tableau d'indices est un tableau carré
# on récupère un tableau carré

indices = np.array([[2, 2],
                    [2, 2]])

# à votre avis on obtient quoi ?
valeurs_d1[indices]

donc si on essaie de formaliser un peu, lorsque valeurs est de dimension 1

valeurs[indices] aura un sens si

• valeurs est de dimension 1
• indices ne contient que des entiers, qui sont des indices valables dans valeurs
• et alors le résultat est un tableau de la même forme que indices

valeurs en dimension 2¶

valeurs_d2 = np.arange(4)+10*np.arange(4).reshape((4, 1))
valeurs_d2

c’est bien sûr la même logique
sauf que cette fois on va avoir envie de .. passer deux tableaux d’indices, puisque valeurs est de dimension 2

avec deux indices de dim 1¶

indices_i = np.array([1, 2, 0, 3])
indices_j = np.array([0, 2, 1, 3])

valeurs_d2[indices_i, indices_j]

avec deux indices de dim 2¶

bien sûr on peut aussi utiliser des indices de formes en dimensions supérieures

indices_i = np.array([[0, 1],
                      [2, 2]])
indices_j = np.array([[0, 0],
                      [3, 3]])

valeurs_d2[indices_i, indices_j]

avec un seul indice¶

on peut même ne donner qu’un seul indice !

souvenez-vous, dans le cas hyper simple où vous avez un tableau de 2 dimension et que vous écrivez array[2], vous récupérez la deuxième ligne

ici ça va être pareil: le résultat a une dimension de plus que le tableau d’indices, pour pouvoir ranger à chaque fois toute la ligne valeurs[i]

valeurs_d2

indices_i = np.array([[0, 2],
                      [1, 3]])

avant d’exécuter la prochaine cellule, essayez de calculer mentalement sa forme

si on avait donné deux indices, on aurait obtenu un tableau carré 2x2 mais comme il manque une dimension, à chaque coordonnée (i, j) dans le tableau d’indices, on va récupérer une ligne (qui dans notre tableau de valeurs est de longueur 4)

donc le résultat est de forme ...

r = valeurs_d2[indices_i]
r

# du coup on 'ajoute' une dimension 4 au résultat

print("si on faisait une indexation complète on obtiendrait", indices_i.shape)
print("l'indexation partielle nous donne ici", r.shape)

si on faisait une indexation complète on obtiendrait (2, 2)
l'indexation partielle nous donne ici (2, 2, 4)

exemple: une colormap¶

c’est cette technique que nous avons utilisée dans le TP ‘image-2’, pour coder la fonction patchwork

imaginons qu’on a en entrée 5 couleurs (en comptant la couleur de remplissage);
et qu’on doit remplir un rectangle de 2 x 3 patches

et faisons pour commencer abstraction de la taille de chaque patch

• on commence par calculer un array de forme 5 x 3 qui contient les rgb des 5 couleurs; on l’appelle la colormap parce que chaque couleur va pouvoir ensuite être codée par un index (entre 0 et 4)

• puis on fabrique un tableau qui a la forme du patchwork (2x3 donc pour commencer) et dans chaque case le rang de la couleur qu’on veut

• et on obtient le résultat par simple indexation

colormap = np.array([
    [255, 0, 0],     # 'red'
    [0, 255, 0],     # 'green'
    [0, 0, 255],     # 'blue'
    [0, 255, 255],   # 'cyan'
    [127, 127, 127], # 'grey background'
])

pattern = np.array([
    [0, 1, 2],
    [3, 4, 4],
])

import matplotlib.pyplot as plt
plt.imshow(colormap[pattern]);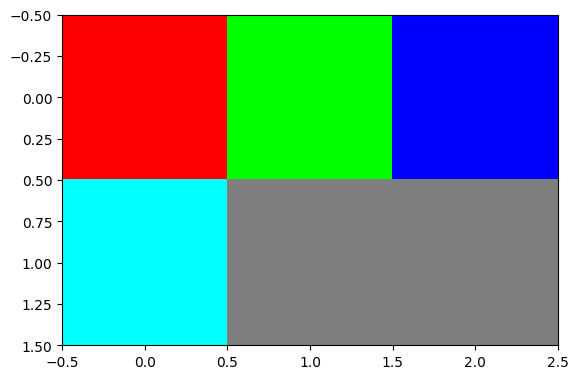

si on prend en compte la taille des patches, le tableau pattern devient un peu plus compliqué, mais c’est toujours le même principe :

pattern2 = np.array([
    [0, 0, 1, 1, 2, 2],
    [0, 0, 1, 1, 2, 2],
    [3, 3, 4, 4, 4, 4],
    [3, 3, 4, 4, 4, 4],
])

plt.imshow(colormap[pattern2]);